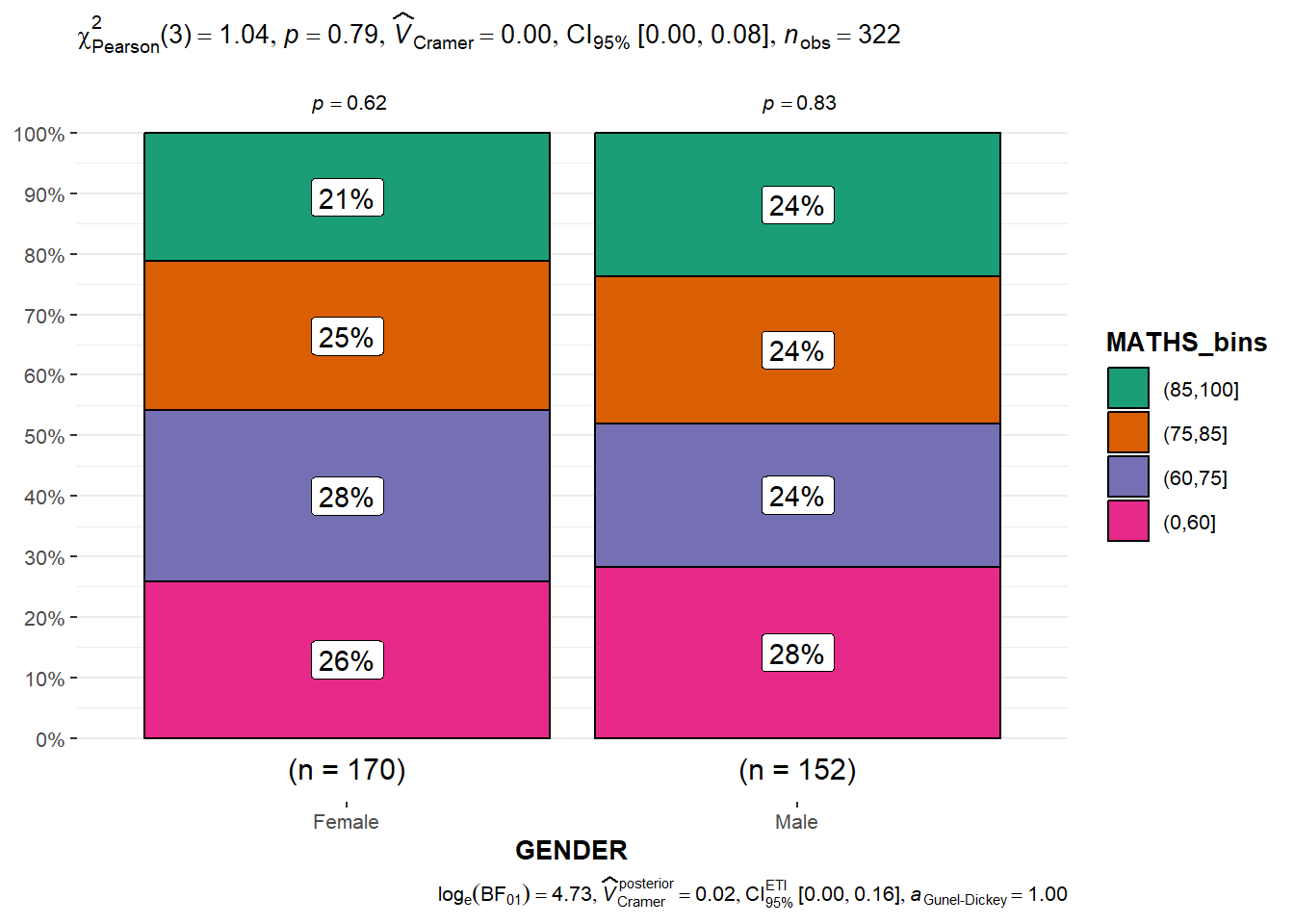pacman::p_load(ggstatsplot, tidyverse)10 Visual Statistical Analysis
10.1 Learning Outcome
In this hands-on exercise, you will gain hands-on experience on using:
ggstatsplot package to create visual graphics with rich statistical information,
performance package to visualise model diagnostics, and
parameters package to visualise model parameters
10.2 Visual Statistical Analysis with ggstatsplot
ggstatsplot 
is an extension of ggplot2 package for creating graphics with details from statistical tests included in the information-rich plots themselves.
- To provide alternative statistical inference methods by default.
- To follow best practices for statistical reporting. For all statistical tests reported in the plots, the default template abides by the [APA](https://my.ilstu.edu/~jhkahn/apastats.html) gold standard for statistical reporting. For example, here are results from a robust t-test: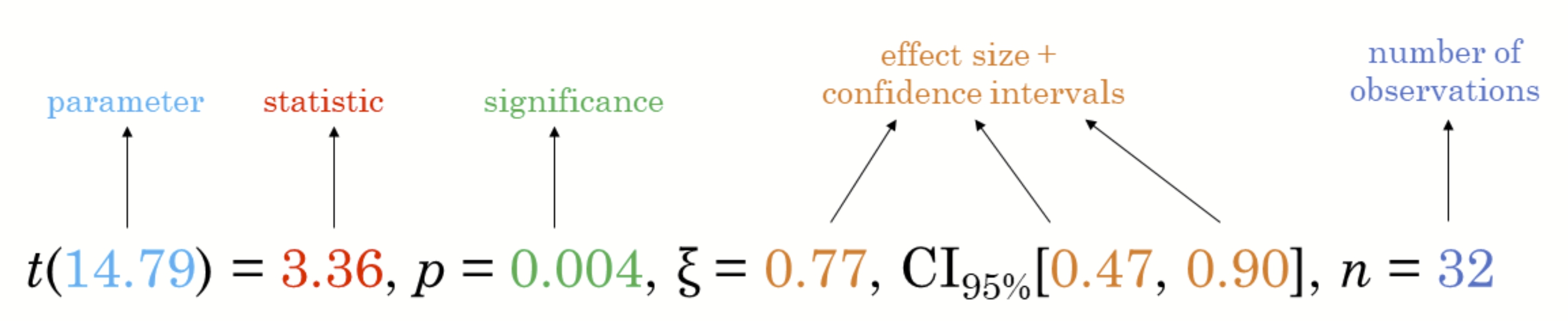
10.3 Getting Started
10.3.1 Installing and launching R packages
In this exercise, ggstatsplot and tidyverse will be used.
10.3.2 Importing data
Do-It-Yourself
Importing Exam.csv data by using appropriate tidyverse package.
# A tibble: 322 × 7
ID CLASS GENDER RACE ENGLISH MATHS SCIENCE
<chr> <chr> <chr> <chr> <dbl> <dbl> <dbl>
1 Student321 3I Male Malay 21 9 15
2 Student305 3I Female Malay 24 22 16
3 Student289 3H Male Chinese 26 16 16
4 Student227 3F Male Chinese 27 77 31
5 Student318 3I Male Malay 27 11 25
6 Student306 3I Female Malay 31 16 16
7 Student313 3I Male Chinese 31 21 25
8 Student316 3I Male Malay 31 18 27
9 Student312 3I Male Malay 33 19 15
10 Student297 3H Male Indian 34 49 37
# ℹ 312 more rows10.3.3 One-sample test: gghistostats() method
In the code chunk below, gghistostats() is used to to build an visual of one-sample test on English scores.
set.seed(1234)
gghistostats(
data = exam,
x = ENGLISH,
type = "bayes",
test.value = 60,
xlab = "English scores"
)
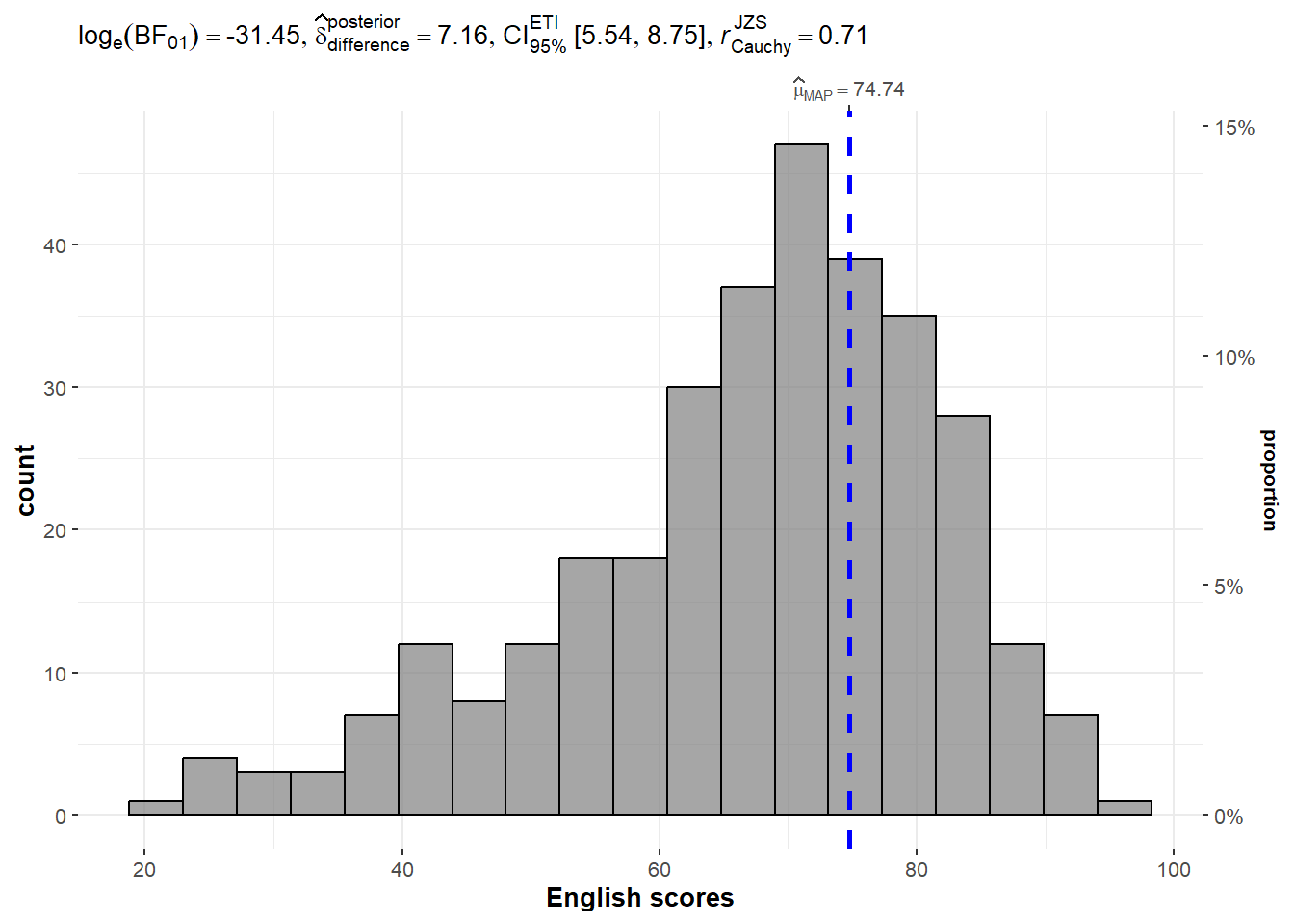
Default information: - statistical details - Bayes Factor - sample sizes - distribution summary
10.3.4 Unpacking the Bayes Factor
A Bayes factor is the ratio of the likelihood of one particular hypothesis to the likelihood of another. It can be interpreted as a measure of the strength of evidence in favor of one theory among two competing theories.
That’s because the Bayes factor gives us a way to evaluate the data in favor of a null hypothesis, and to use external information to do so. It tells us what the weight of the evidence is in favor of a given hypothesis.
When we are comparing two hypotheses, H1 (the alternate hypothesis) and H0 (the null hypothesis), the Bayes Factor is often written as B10. It can be defined mathematically as
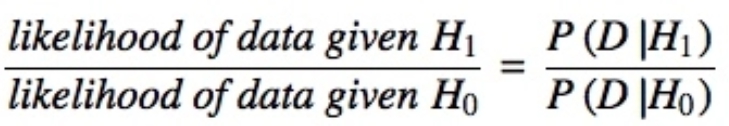
- The Schwarz criterion is one of the easiest ways to calculate rough approximation of the Bayes Factor.
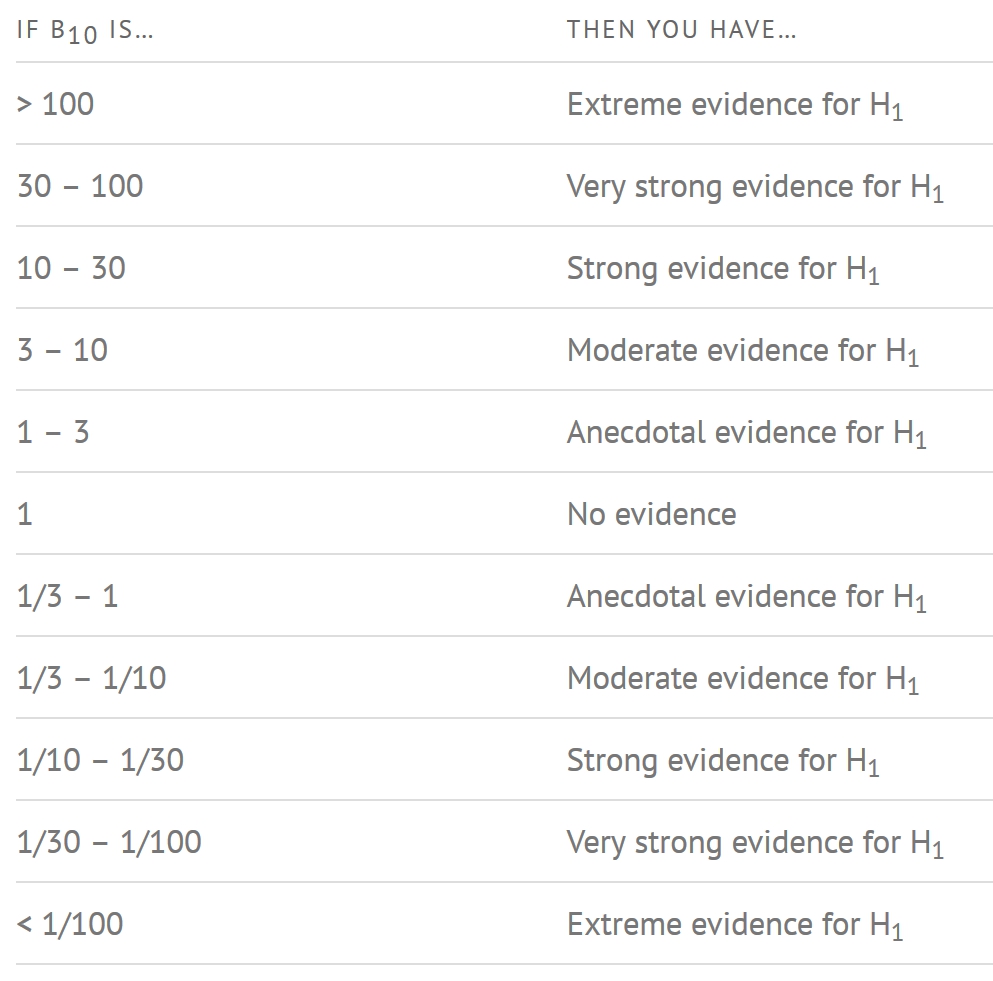
10.3.5 How to interpret Bayes Factor
A Bayes Factor can be any positive number. One of the most common interpretations is this one—first proposed by Harold Jeffereys (1961) and slightly modified by Lee and Wagenmakers in 2013:
10.3.6 Two-sample mean test: ggbetweenstats()
In the code chunk below, ggbetweenstats() is used to build a visual for two-sample mean test of Maths scores by gender.
ggbetweenstats(
data = exam,
x = GENDER,
y = MATHS,
type = "np",
messages = FALSE
)
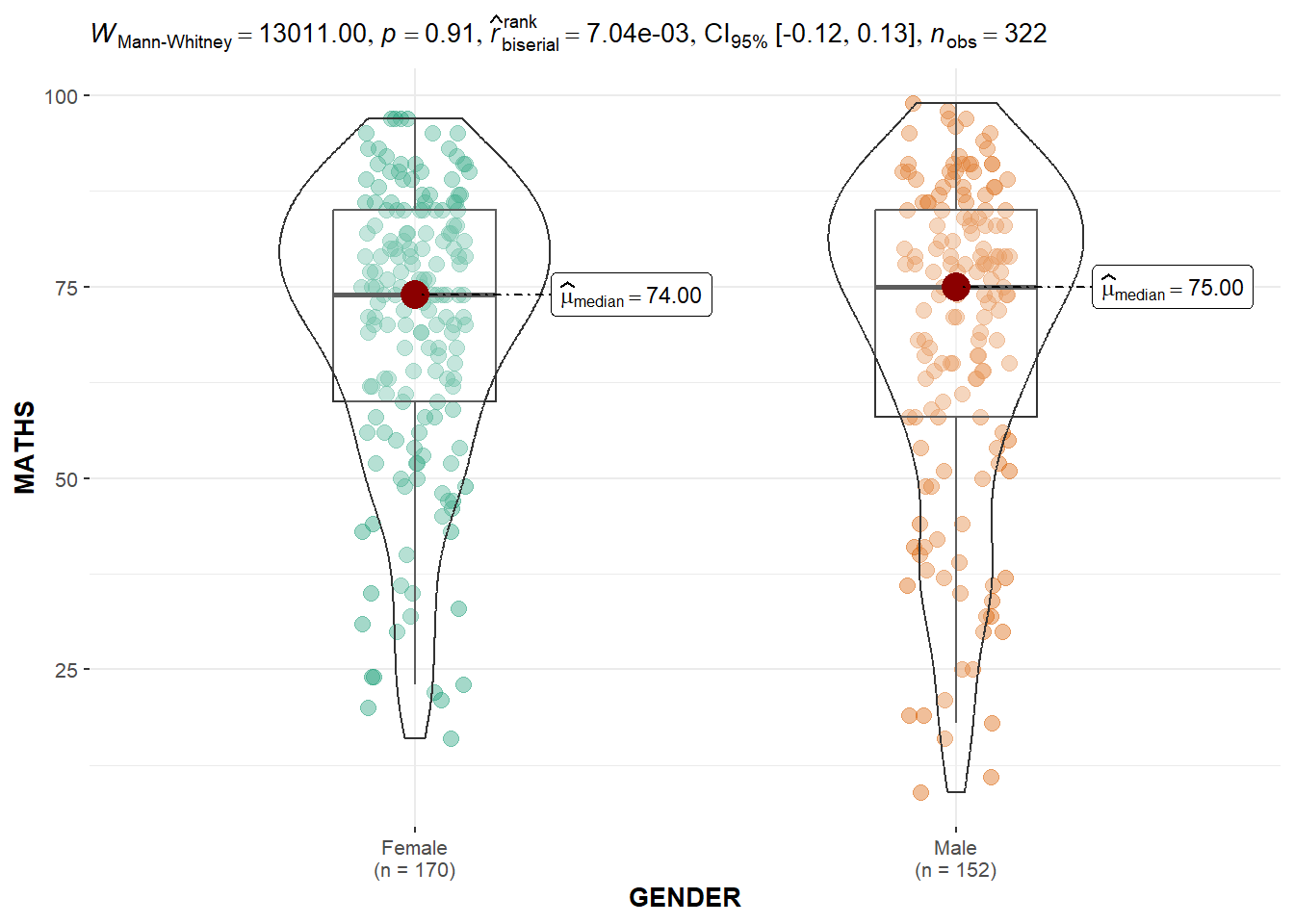
Default information: - statistical details - Bayes Factor - sample sizes - distribution summary
10.3.7 Oneway ANOVA Test: ggbetweenstats() method
In the code chunk below, ggbetweenstats() is used to build a visual for One-way ANOVA test on English score by race.
ggbetweenstats(
data = exam,
x = RACE,
y = ENGLISH,
type = "p",
mean.ci = TRUE,
pairwise.comparisons = TRUE,
pairwise.display = "s",
p.adjust.method = "fdr",
messages = FALSE
)
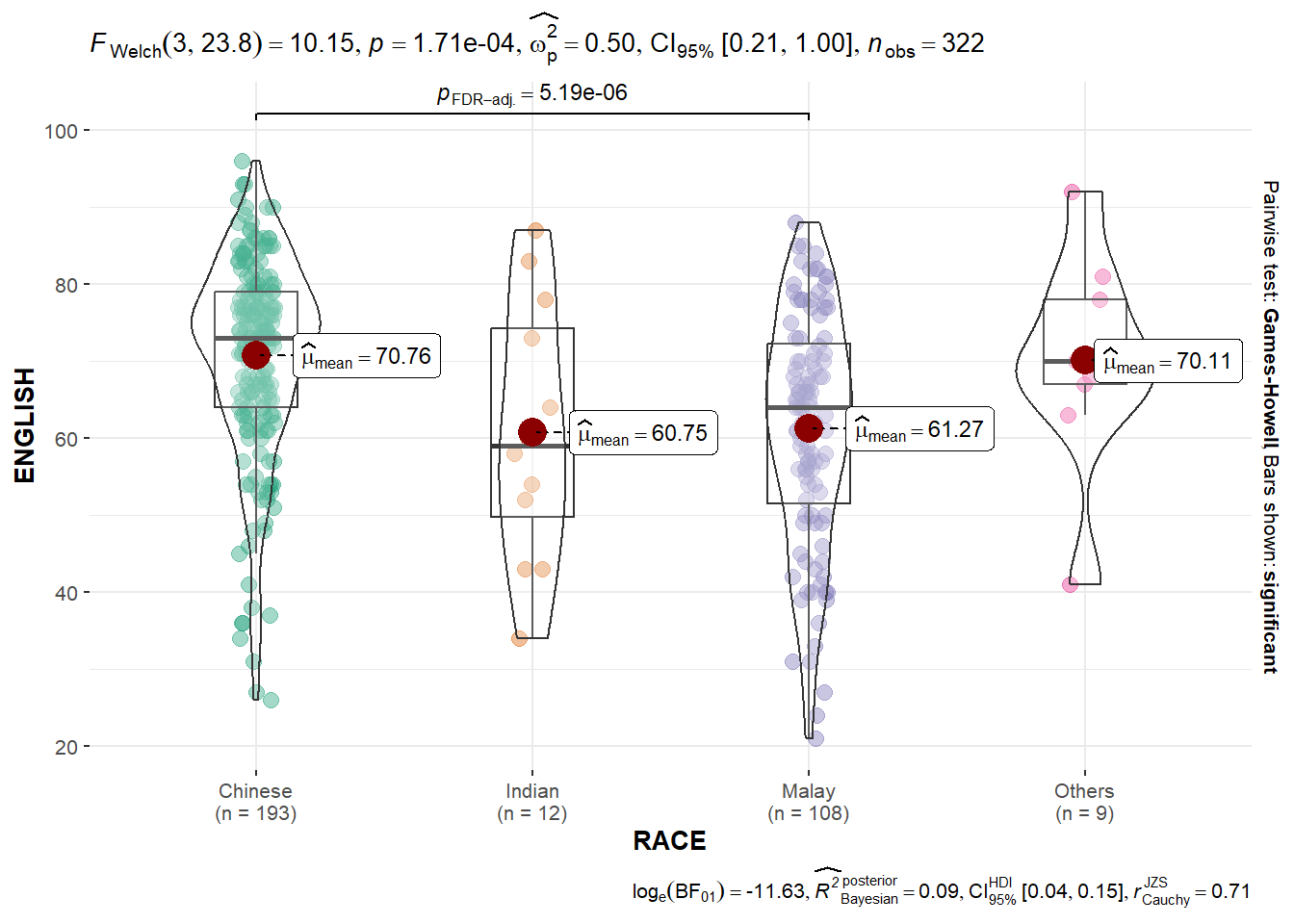
- “ns” → only non-significant
- “s” → only significant
- “all” → everything
10.3.7.1 ggbetweenstats - Summary of tests
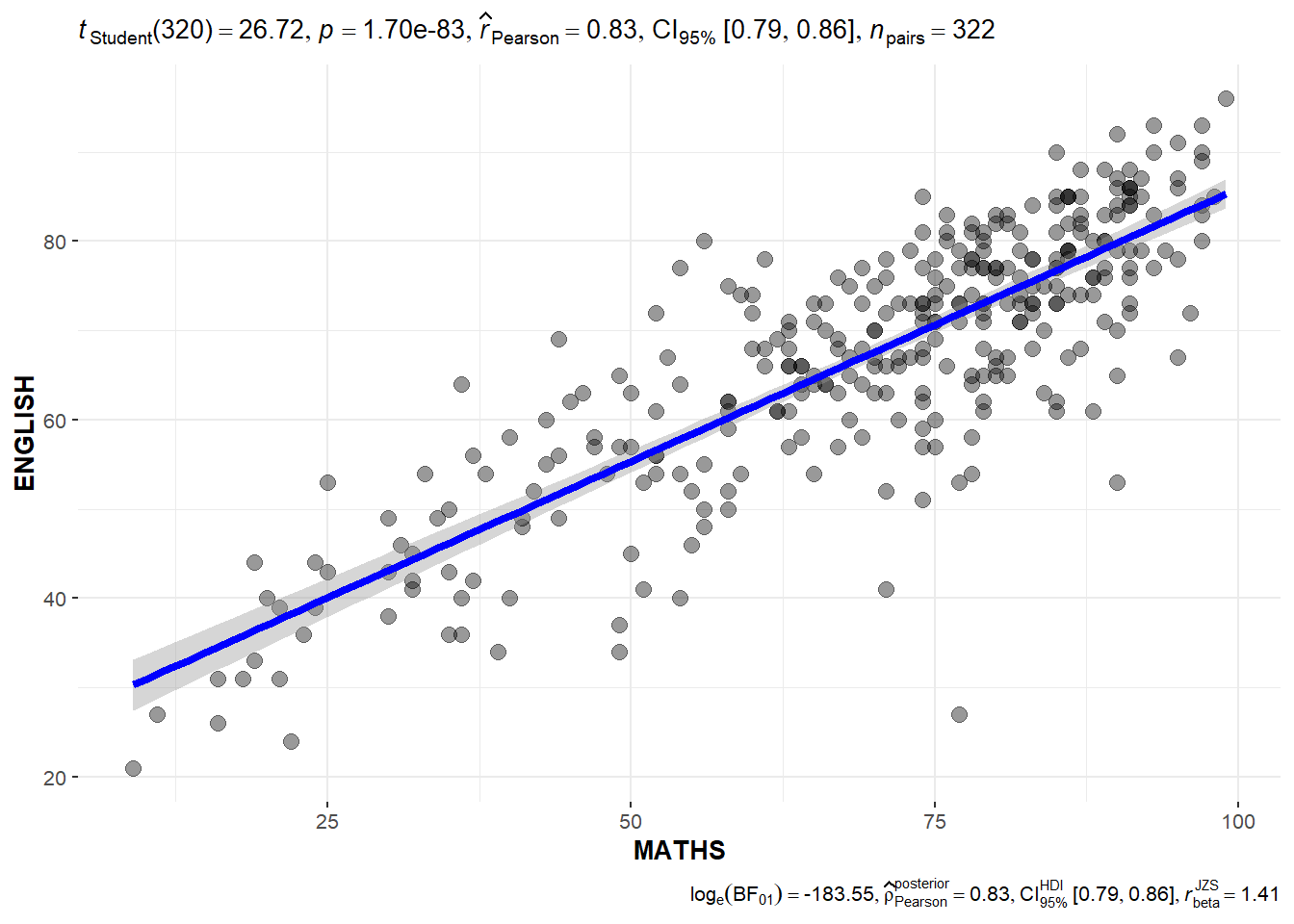
10.3.8 Significant Test of Correlation: ggscatterstats()
In the code chunk below, ggscatterstats() is used to build a visual for Significant Test of Correlation between Maths scores and English scores.
ggscatterstats(
data = exam,
x = MATHS,
y = ENGLISH,
marginal = FALSE,
)
10.3.9 Significant Test of Association (Depedence) : ggbarstats() methods
In the code chunk below, the Maths scores is binned into a 4-class variable by using cut().
exam1 <- exam %>%
mutate(MATHS_bins =
cut(MATHS,
breaks = c(0,60,75,85,100))
)In this code chunk below ggbarstats() is used to build a visual for Significant Test of Association
ggbarstats(exam1,
x = MATHS_bins,
y = GENDER)
10.4 Visualising Models
In this section, you will learn how to visualise model diagnostic and model parameters by using parameters package.
- Toyota Corolla case study will be used. The purpose of study is to build a model to discover factors affecting prices of used-cars by taking into consideration a set of explanatory variables.
10.5 Getting Started
10.6 Installing and loading the required libraries
Do-It-Yourself
pacman::p_load(readxl, performance, parameters, see)10.6.1 Importing Excel file: readxl methods
In the code chunk below, read_xls() of readxl package is used to import the data worksheet of ToyotaCorolla.xls workbook into R.
car_resale <- read_xls("data/ToyotaCorolla.xls",
"data")
car_resale# A tibble: 1,436 × 38
Id Model Price Age_08_04 Mfg_Month Mfg_Year KM Quarterly_Tax Weight
<dbl> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 81 TOYOTA … 18950 25 8 2002 20019 100 1180
2 1 TOYOTA … 13500 23 10 2002 46986 210 1165
3 2 TOYOTA … 13750 23 10 2002 72937 210 1165
4 3 TOYOTA… 13950 24 9 2002 41711 210 1165
5 4 TOYOTA … 14950 26 7 2002 48000 210 1165
6 5 TOYOTA … 13750 30 3 2002 38500 210 1170
7 6 TOYOTA … 12950 32 1 2002 61000 210 1170
8 7 TOYOTA… 16900 27 6 2002 94612 210 1245
9 8 TOYOTA … 18600 30 3 2002 75889 210 1245
10 44 TOYOTA … 16950 27 6 2002 110404 234 1255
# ℹ 1,426 more rows
# ℹ 29 more variables: Guarantee_Period <dbl>, HP_Bin <chr>, CC_bin <chr>,
# Doors <dbl>, Gears <dbl>, Cylinders <dbl>, Fuel_Type <chr>, Color <chr>,
# Met_Color <dbl>, Automatic <dbl>, Mfr_Guarantee <dbl>,
# BOVAG_Guarantee <dbl>, ABS <dbl>, Airbag_1 <dbl>, Airbag_2 <dbl>,
# Airco <dbl>, Automatic_airco <dbl>, Boardcomputer <dbl>, CD_Player <dbl>,
# Central_Lock <dbl>, Powered_Windows <dbl>, Power_Steering <dbl>, …Notice that the output object car_resale is a tibble data frame.
10.6.2 Multiple Regression Model using lm()
The code chunk below is used to calibrate a multiple linear regression model by using lm() of Base Stats of R.
model <- lm(Price ~ Age_08_04 + Mfg_Year + KM +
Weight + Guarantee_Period, data = car_resale)
model
Call:
lm(formula = Price ~ Age_08_04 + Mfg_Year + KM + Weight + Guarantee_Period,
data = car_resale)
Coefficients:
(Intercept) Age_08_04 Mfg_Year KM
-2.637e+06 -1.409e+01 1.315e+03 -2.323e-02
Weight Guarantee_Period
1.903e+01 2.770e+01 10.6.3 Model Diagnostic: checking for multicolinearity:
In the code chunk, check_collinearity() of performance package.
check_collinearity(model)# Check for Multicollinearity
Low Correlation
Term VIF VIF 95% CI Increased SE Tolerance Tolerance 95% CI
KM 1.46 [ 1.37, 1.57] 1.21 0.68 [0.64, 0.73]
Weight 1.41 [ 1.32, 1.51] 1.19 0.71 [0.66, 0.76]
Guarantee_Period 1.04 [ 1.01, 1.17] 1.02 0.97 [0.86, 0.99]
High Correlation
Term VIF VIF 95% CI Increased SE Tolerance Tolerance 95% CI
Age_08_04 31.07 [28.08, 34.38] 5.57 0.03 [0.03, 0.04]
Mfg_Year 31.16 [28.16, 34.48] 5.58 0.03 [0.03, 0.04]check_c <- check_collinearity(model)
plot(check_c)
10.6.4 Model Diagnostic: checking normality assumption
In the code chunk, check_normality() of performance package.
model1 <- lm(Price ~ Age_08_04 + KM +
Weight + Guarantee_Period, data = car_resale)check_n <- check_normality(model1)plot(check_n)
10.6.5 Model Diagnostic: Check model for homogeneity of variances
In the code chunk, check_heteroscedasticity() of performance package.
check_h <- check_heteroscedasticity(model1)plot(check_h)
10.6.6 Model Diagnostic: Complete check
We can also perform the complete by using check_model().
check_model(model1)
10.6.7 Visualising Regression Parameters: see methods
In the code below, plot() of see package and parameters() of parameters package is used to visualise the parameters of a regression model.
plot(parameters(model1))
10.6.8 Visualising Regression Parameters: ggcoefstats() methods
In the code below, ggcoefstats() of ggstatsplot package to visualise the parameters of a regression model.
ggcoefstats(model1,
output = "plot")